INTRODUCTION
The factorial of an integer N, denoted by N! is the product of all positive integers less than or equal to n. Factorial does not exist for negative numbers and factorial of 0 is 1.
N! = 1 x 2 x 3 x 4....x (N-2) x (N-1) x N
For Example
5! = 5 * 4 * 3 * 2 * 1 = 120.
We can use recursion to calculate factorial of a number because factorial calculation obeys recursive sub-structure property. Let factorial(N) is a function to calculate and return the value of N!. To find factorial(N) we can first calculate factorial(N-1) then multiply it with N.
N! = 1 x 2 x 3 x 4....x (N-2) x (N-1) x N
N! = (N-1)! x N
factorial(N) = factorial(N-1) x N
Function factorial(N) reduces the problem of finding factorial of a number N into sub-problem of finding factorial on N-1. It keeps on reducing the domain of the problem until N becomes zero.
Algorithm:
Step 1: START
Step 2: READ N
Step 3: IF N==0 OR N==1 THEN GO TO Step 4
ELSE RETURN N*FACT N-1
Step 4: RETURN 1
Step 5: PRINT FACT
Step 6: STOP
Program TO factorial of A Number Using Recursion:
#include<stdio.h>
#include<conio.h>
int fact(int);
main()
{
int n;
printf("\n Enter The Number:");
scanf("%d",&n);
printf("\n The Factorial value is: %d",fact(n));
getch();
}
int fact(int n)
{
if(n==0||n==1)
return 1;
else
return n*fact(n-1);
}
Output:
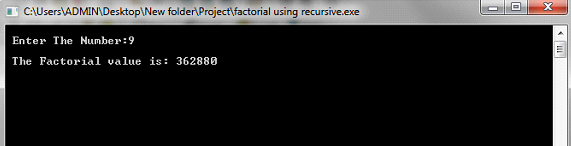
1st case:
2nd case:
3rd case:
The factorial of an integer N, denoted by N! is the product of all positive integers less than or equal to n. Factorial does not exist for negative numbers and factorial of 0 is 1.
N! = 1 x 2 x 3 x 4....x (N-2) x (N-1) x N
For Example
5! = 5 * 4 * 3 * 2 * 1 = 120.
We can use recursion to calculate factorial of a number because factorial calculation obeys recursive sub-structure property. Let factorial(N) is a function to calculate and return the value of N!. To find factorial(N) we can first calculate factorial(N-1) then multiply it with N.
N! = 1 x 2 x 3 x 4....x (N-2) x (N-1) x N
N! = (N-1)! x N
factorial(N) = factorial(N-1) x N
Function factorial(N) reduces the problem of finding factorial of a number N into sub-problem of finding factorial on N-1. It keeps on reducing the domain of the problem until N becomes zero.
Algorithm:
Step 1: START
Step 2: READ N
Step 3: IF N==0 OR N==1 THEN GO TO Step 4
ELSE RETURN N*FACT N-1
Step 4: RETURN 1
Step 5: PRINT FACT
Step 6: STOP
Program TO factorial of A Number Using Recursion:
#include<stdio.h>
#include<conio.h>
int fact(int);
main()
{
int n;
printf("\n Enter The Number:");
scanf("%d",&n);
printf("\n The Factorial value is: %d",fact(n));
getch();
}
int fact(int n)
{
if(n==0||n==1)
return 1;
else
return n*fact(n-1);
}
Output:
1st case:
2nd case:
3rd case:
Discussion
When it came to teaching recursion in programming languages in the 1980s and 1990s, the factorial function n!nn! was the classic example to explain the concept.
Usually left unexplained, in a mathematical paper or book one might encounter an explanation for then !nn! shorthand for this function along the lines of
(with 0!=1010!=1) while a computer programming book might say something like n!=1×2×…×(n-1)×nn12normal-…n1nn!=1\times 2\times\ldots\times(n-1)\times n (with the same assignment for zero factorial). Either of these suggests implementation with some kind of FOR loop.
The recurrence relation n!=(n-1)!nnn1nn!=(n-1)!n with n>1n1n>1 and 1!=1111!=1 suggests a recursive implementation.









1 Comments
15CD20D45E
ReplyDeletetakipçi satın al
Başkasına Takipçi Gönderme
Para ile Takipçi
Sanal Numara
Coin Kazanma